0
留言稍后联系!

摘要 GIS 局部放电模式识别是其状态评估的重要部分,搭建了 252kVGIS 局部放电超高频检测仿真实验平台,模拟了 4 种典型的 GIS 局部放电模型,并通过试验建立了相应的超高频信号图谱数据库,然后根据信号特点提取了 26 个原始特征量;采用主成分分析法对特征空间进行降维处理,最终得到 10 个新的特征量,将原始特征量和降维后的特征量分别输入到多分类相关向量机(M-RVM)中进行分析,结果表明,以降维后的特征量作为输入量,其识别率要高于降维前的;并且采用 BN、SVM 和 M-RVM 三种分类器进行对比分析,结果表明,无论是采用原始特征参量还是降维后的参量作为输入量,M-RVM 方法的识别率都是最高,其中降维后的识别率大于 85%。
关键词:气体绝缘组合电器 局部放电 主成分分析 多分类相关向量机 模式识别
1 引言
局部放电(Partial Discharge,PD)是 SF6 气体绝缘组合电器(Gas Insulated Switchgear,GIS)绝缘劣化的主要表现形式,不同放电类型所反映的绝缘劣化机理不同,而且不同放电类型对 GIS 绝缘造成的损害程度不同[1,2],因此,对 GIS 局部放电进行模式识别已经成为 GIS 状态评估方面的重要部分[3-5]。
在局部放电模式识别领域,主要是从原始特征中选出对分类有利的特征子集,常见的方法有统计特征参数法[6,7]、波形特征参数法[8]和图像矩特征参数法等[9]。但是,在局部放电特征参数提取的过程中,得到的特征变量往往数量较多,造成特征空间维数较高,不仅给分类器带来负担,甚至造成识别率下降,所以对特征空间进行降维是必要的,而主成分分析法作为一种统计特征参数法[10],其最大的优点就是有效将高维特征空间降到低维空间,已经在很多领域取得了较好的效果,本文采用该方法对 GIS 局部放电特征空间算子进行分析。
局部放电模式识别不仅需要提取有利的特征量,选择合适的分类器也是至关重要的。GIS 局部放电模式识别是一个多分类问题,而 Damoulasy 等人提出了多分类相关向量机(Milticlass Relevance Vector Machine,M-RVM),该方法基函数权值少数非零,诊断速度快,另外可有效解决小样本、高维、非线性分类问题,更重要的是该方法通过引入多项概率似然函数,可以直接实现多分类[11,12]。因此,本文选择 M-RVM 作为 GIS 局部放电模式识别分类器。
在 GIS 局部放电检测中,超高频(Ultra High Frequency,UHF)法检测的是超高频波段(300~ 3 000MHz),抗干扰能力强,灵敏度高[13],基于此,本文在实验室模拟了 4 种典型的局部放电模型,采用 UHF 法获取了相应的局部放电信号,通过主成分分析法对 UHF 信号统计参量进行降维处理,提取了新的特征量,然后用多分类相关向量机对 GIS 局部放电进行模式识别。
2 局部放电试验
2.1 试验平台
采用自行设计的 252kVGIS 局部放电仿真平台,整个平台长 5m,高 4.15m,为了方便试验和节约 SF6 气体,该平台采用盆式绝缘子将腔体隔开成为多个单独的小气室;超高频探头的检测频段为 300~1 500MHz,试验电路接线示意图和 GIS 局部放电仿真平台结构图分别如图 1 和图 2 所示:
针对 GIS 局部放电的特点,设计了 4 种典型的放电模型:尖端放电、内部放电、悬浮放电和沿面放电,相关结构如图 3 所示。
模型参数如下:尖端放电模型,高压针电极曲率半径为 0.5mm,锥角 30°,尖长 15mm,电极间距离为 10mm;内部放电模型,放电模型上下 2 层均采用厚 3mm 的环氧树脂板,中间采用 1mm 厚的环氧树脂板作绝缘介质,绝缘板上有直径为 10mm 的圆孔,绝缘板之间用环氧树脂胶粘结;悬浮放电模型,接地电极上放直径 100mm,厚 5mm 的环氧树脂板,环氧树脂板上面靠近边缘处放置直径 10mm,高10mm 的铜柱;沿面放电模型,两个板电极之间纵向放置一个直径 10mm,长 10mm 的环氧树脂棒。为了减小表面毛刺的影响,电极表面和边缘均打磨光滑,为了消除电极引线处的放电,设计并加工了光滑的球形螺帽。
2.2 超高频信号特征参量
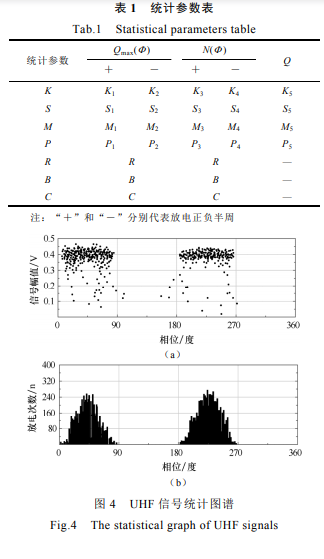
根据 2.1 节实验获取的 UHF 信号,得到了局部放电次数 N、总放电量 QT、最大放电量 Qmax 等统计参数,针对局部放电模式识别的需求,最终选择局部放电 UHF 信号最大放电幅值相位分布 Qmax()、放电重复率相位分布 N() 及局部放电幅值分布 Q 三个不同二维图谱,分别提取出包括局部峰个数 P、偏斜度 S、放电量因数 R、陡峭度 K、相位中值 M、相位不对称度 B、互相关系数 C 共 26 个统计算子,这些统计参数从不同角度描述谱图特性,同时为了消除量纲的影响,各个参数均采用了标准化处理。各特征参数对应关系如表 1 所示。获取的典型 UHF 图谱如图 4 所示。
3 参数主成分及因子分析
2.2 节中得到的特征参数共有 26 个,构成的特征空间维数很高,参数之间的相关性较大,可能存在信息冗余,直接送入分类器进行模式识别不但会给分类器带来较大的负担,而且也可能产生比较大的误差。主成分及因子分析方法使得提取出的特征量既可以全面表征放电谱图特征,同时又降低了特征空间维数,减小了分类器的负担。
3.1 因子相关性分析
大量的特征参量,可能造成信息重叠,通过因子相关性分析,可以找出反映变量之间共同特性的少数公共因子变量,从而可以判断数据是否适合进行主成分分析。以特征量 K1~K5 为例进行相关性分析。常用的检验方法有 KMO 检验和 Bartlett 球形检验,KMO 是用于检验因子分析是否适用的指标,若它在 0.5~1 之间,表示适合;小于 0.5 表示不适合。 Bartlett 球形检验是通过 x2 检验来完成对变量之间是否相互独立的检验。若统计量取值较大,且对应的显著性水平较小,则因子分析是适用的。运用 SPSS 软件对统计出的 K1~K5 变量进行分析,输出检验结果下:KMO 的值 0.713,变量之间存在较强的偏相关性;Bartlett 球形检验为 127.13,显著性水平为 0,拒绝零假设,变量之间适合进行因子分析,可以进行主成分分析。
3.2 协方差矩阵的主成分分析
针对陡峭度 5 个特征参数,通过求解协方差矩阵的特征值和与之对应的特征向量,将原来的相关向量进行线性变换。对得到的特征值进行分析,选择值大于 1 的特征根作为主成分进行分析,从而达到降维的目的。表 2 列出了协方差矩阵的特征值及方差贡献率,图 5 为贡献率随主成分变化趋势图。
由图 5 分析得到,从第 3 个主成分开始,贡献率变化趋势已趋于平稳,且贡献率逐渐减小,其贡献可忽略不计。因此,取前 2 个主成分是比较合适的,可以很好地反映绝大部分变量信息。这样由原来的 5 个指标转化为 2 个新指标,起到了降维作用。 SPSS 分析软件得到主成分系数如表 3 所示。
根据上面的线性组合可以得到主成分的值,同样的方法可以计算出局部峰个数 P、偏斜度 S、放电量因数 R、相位中值 M、相位不对称度 B、互相关系数 C 的主成分,提取出的成分如表 4 所示。通过主成分分析,提取出 26 个特征变量的 10 个主成分因子,各参数的信息表征率均在 76%以上。
4 基于 M-RVM 的局部放电模式识别
根据 2.1 节可知,本文 GIS 局部放电模型共分为 4 类,是一个多分类问题,而多分类相关向量机(Milticlass Relevance Vector Machine,M-RVM)是 Damoulasy 等人在二分类核函数学习、高斯过程组合协方差函数方法以及高斯先验处理多项概率似然函数方法的基础上,提出的一种可以直接实现多分类的方法,只要采用一个 M-RVM 分类器即可实现 GIS 的多种状态类别的识别。
相关知识推荐:论文投稿需要共同作者确认吗
M-RVM 通常采用 0-1 的向量形式来表示类别,设需要识别的 GIS 状态类别为 L 种,则可以采用 L 维的 0-1 列向量的形式来表示该 L 种状态的类别标签。本文中,GIS 局部放电由尖端放电、内部放电、悬浮放电和沿面放电 4 种放电模型构成,分别采用 4 维列向量(0,0,0,1)T 、(0,0,1,0)T 、(0,1,0,0)T 、(1,0,0,0)T 作为 GIS 上述 4 种状态的类别标签。
4.2 特征量选择
由于基于 M-RVM 的模式分类方法采用一个 M-RVM 分类器识别 GIS 的多种局部放电模式类别,因此要求选取的输入特征变量能够同时表征所要甄别的多种状态类别,而根据第 2 和第 3 节已经获取了表征 GIS 局部放电模式的 26 个原始特征量以及采用主成分分析法降维后的 10 个特征量,为了对比分析,分别输入这两种特征参数,输入参数均采用了标准归一化。
4.3 选取核函数
M-RVM 通常采用的核函数有:线性核函数,多项式核函数和径向基核函数(RBF)等。该文选择模式识别中通常采用的 RBF 核函数。
4.4 诊断输出
M-RVM 诊断方法的诊断输出是 GIS 隶属于各种状态类别的概率值,对于把 GIS 状态划分为 L 种状态类别的情况,输出可以采用 L 维行向量的形式,该 L 维行向量中的元素分别代表 GIS 隶属于 L 种状态类别的概率,其对应关系与 M-RVM 分类器学习时状态类别采用的表示方法有关。本文把 GIS 绝缘故障状态设置为 4 类,对应于 GIS 局部放电状态类别的上述表达形式。M-RVM 分类器的诊断输出向量模式为:[PZ,PN,PX,PY],其中 PZ,PN,PX,PY 分别代表 GIS 的状态为尖端放电、内部放电、悬浮放电和沿面放电的概率值,记输出向量的索引集为 I={Z, N, X, Y }。
4.5 基于 M-RVM 的 GIS 局部放电模式识别过程
基于 M-RVM 的 GIS 局部放电模式识别具体分类过程如下,流程如图 7 所示。
(1)依据研究问题的特点,划分 GIS 的局部放电模式状态,并确定各种状态相应的表示方法。
(2)依据获取的 GIS 局部放电参数,选取 M-RVM 分类器的输入特征变量,确定 M-RVM 分类器的诊断输出表示方式。
(3)选取样本数据[ ,] X t 。
(4)选取核函数并确定核函数参数。
(5)将样本数据分为训练集 tr tr [ ,] X t 和测试集 te te [ ,] X t ,进行 M-RVM 模型学习和测试。表 5 和表 6 给出采用 BN、SVM 和 M-RVM 方法的 GIS 模式识别的结果。其中,SVM 核函数选用 RBF,采用“一对一”的分类方法;BN 采用贝叶斯分类器。BN、SVM 和 M-RVM 方法均按 4.2 节确定输入向量,得到的 3 个分类器错分率曲线如图 8 所示。
通过上面的曲线可以看出 M-RVM 分类器的错分率明显低于另外两种算法,最终得到的识别结果如表 5 和表 6 所示。
5 结论
文章设计了 252kVGIS 局部放电超高频检测仿真平台,模拟了 4 种典型的 GIS 局部放电模型,获取了相应的超高频信号统计特征量,采用主成分分析法对原始特征空间进行了降维处理,结合多分类相关向量机对 GIS 局部放电进行了模式识别,取得了如下结论:
(1)根据 4 种典型的放电模型,获取了 UHF 信号中最大放电幅值相位分布 Qmax()、放电重复率相位分布 N() 及局部放电幅值分布 Q 三个不同二维图谱,并且从统计数据中提取了 26 个原始特征量。
(2)采用主成分分析法可以有效的实现特征空间的降维处理,将原始的 26 个特征量降为 10 个新的特征量,并且以新的特征量作为输入量进行 GIS 局部放电模式识别,其识别率大于 85%。
(3)采用多分类相关向量机作为模式分类器,无论是采用原始的 26 个特征参量还是降维后的 10 个特征参量,其识别率都要高于 BN、SVM 分类器。——论文作者:律方成 金 虎 王子建 张 波
参考文献
[1] 司文荣, 李军浩, 袁鹏, 等. 基于波形非线性映射的多局部放电脉冲群快速分类[J]. 电工技术学报, 2009, 24(3): 217-228. Si Wenrong, Li Junhao, Yuan Peng, et al. The fast grouping technique of PD sequence based on the nonlinear mapping of pulse shapes[J]. Transactions of China Electrotechnical Society, 2009, 24(3): 217- 228.
[2] 李信, 李成榕, 丁立健, 等. 基于特高频信号检测 GIS 局放模式识别[J]. 高电压技术, 2003, 14(3): 16-20. Li Xin, Li Chengrong, Ding Lijian, et al. Identification of PD patterns in gas insulated swichgear(GIS) based on UHF signals[J]. High Voltage Engineering, 2003, 14(3): 16-20.
[3] 唐炬, 周倩, 许中荣, 等. GIS 特高频局放信号的数学建模[J]. 中国电机工程学报, 2005, 25(19): 106- 110. Tang Ju, Zhou Qian, Xu Zhongrong, et al. Establishment of mathematical model for partial discharge in GIS using UHF method[J]. Proceedings of the CSEE, 2005, 25(19): 106-110.
* 稍后学术顾问联系您