0
发表咨询在线!

摘要:准确提取参数对超级电容储能系统安全、可靠、高效运行具有重要意义。为克服测试系统复杂、有效数据点少、在线提取困难等问题,提出一种通过补偿内阻消除平衡充放电滞回差异的超级电容参数提取方法。该方法充分利用超级电容在充放电过程中由内阻压降引起的容值-端电压曲线不重合的物理特性,从充放电过程的所有数据中准确提取参数,可有效排除动态过程对参数提取精度的影响。理论分析与实验研究表明所提方法能在不同温度与电流条件下准确提取超级电容的等效参数,可为系统性能测试、优化控制以及高效运维提供有效支撑。
关键词:超级电容;参数提取;滞回特性;充放电过程
0 引言
超级电容是一种新型的电能存储装置,具有功率密度大、充放电效率高、循环寿命长、使用温度范围宽、环保等优点[1]。将大功率密度的超级电容与高能量密度的储能元件(如蓄电池、燃料电池)构成混合储能系统可互补利用不同元件的性能优势,广泛应用于电动汽车、船舶电力推进、制动能量回收和新能源发电等场合[2-11]。
超级电容在工作过程中存在可逆的电解液极化过程,其电阻与电容参数受电压、温度、电流等多种因素影响而并非常数。参数变化可能引起充放电效率下降及发热增加,降低能量利用效率及缩短使用寿命。实际工程中,准确提取超级电容等效参数并研究其特性,对系统优化设计以及安全、可靠、高效运行具有重要意义[12-19]。
国内外学者针对超级电容参数提取方法开展过大量研究,现有方法主要集中在阻抗谱法[14]和暂态压降法[15-16]。其中阻抗谱法属于一种离线频域测试的方法,它采用一套专用设备在离线条件下对超级电容注入不同频率的谐波并得到一定频段范围内的阻抗参数。该方法可获得超级电容的阻抗谱并建立系统高阶详细模型,但测试设备十分昂贵。暂态压降法是目前IEC与国家标准规定的超级电容内阻测试方法。该方法利用平衡充放电切换暂态过程中电容电压的变化量 ΔUSC与电流 ISC之比测量电容内阻 Req,即 Req=ΔUSC/ISC。然而由于充放电切换暂态过程很短且内阻压降很小,该方法对测量动态性能及精度要求很高。此外,暂态电压降需根据预设计算起始电压与计算结束电压通过线性反推获取,这对测量设备的精度要求很高。
为克服现有技术的困难,本文从物理特性的角度出发提出一种基于充放电滞回特性的超级电容参数提取方法。该方法可通过超级电容储能系统平衡充放电测试来获取电容器参数信息,其中平衡充放电是指采用相同大小的电流对超级电容进行充放电的一种测试方式。理论上而言,在忽略充放电电流切换引起电压暂降的准稳态条件下超级电容在每次平衡充放电过程中的等效电容 Ceq与其电压 UC特性(即Ceq = f(UC ))应保持一致。但实际系统中,由于内阻压降会引起超级电容容值估算偏差,导致充放电过程中电容-端电压曲线出现滞回现象。基于该物理特性,通过补偿内阻压降来消除滞回特性有望准确获取电容器内阻与电容参数。为验证所提方法的可行性与有效性,开展了实验研究工作,结果表明滞回特性法可准确提取不同工况下的电容等效参数。不同于传统暂态压降法仅利用充放电切换前后个别暂态数据点计算内阻参数,本文提出的方法充分利用超级电容充放电过程中的所有数据,并通过消除滞回特性的方式估算电容参数,从原理上可有效避免动态过程及非线性特性对参数提取精度的影响。作为一种准在线测试技术[19],该方法具有安全、简便、准确等优点,可为系统性能测试、优化控制及高效运维提供支撑。
1 超级电容充放电滞回特性及产生机理
典型的超级电容等效模型如图 1所示,图中 USC 为超级电容端电压。
容-压特性是由超级电容电解液电荷扩散效应引起一种物理特性。
分析理论模型可知,超级电容运行过程中,随着电压增加,电解液中电荷扩散分布梯度逐渐减小(即双电层间距离减小)而容值增大。与理想模型不同,实际超级电容存在内阻压降,端电压与等效电容压降并不完全相等。超级电容充放电过程中内阻压降极性不同,会出现等效电容-端电压特性(即 Ceq = f(USC))曲线无法重合的滞回现象。典型超级电容充放电过程中的容-压滞回特性曲线见附录A图A1。
在 90 A/25 ℃ 条件下对 2.7 V/3 000 F 超级电容进行充放电测试(实验系统详见4.1节),测得的电容器端电压与电流波形如附录 A图 A1(a)所示。若不能准确补偿电容内阻就会引起等效电容电压与容值的估算偏差,形成充放电过程中的容-压曲线滞回偏差,据此特性可利用测量得到的端电压与电流估算超级电容参数。如图 A1(b)中蓝色曲线所示,若忽略电容内阻则会引起充电过程中电容电压偏大而容值偏小,而放电过程则相反,从而形成容-压滞回特性;如图A1(b)中红色曲线所示,准确补偿内阻后可在准稳态条件下有效消除容-压滞回现象。
2 基于滞回特性的超级电容参数提取法
根据超级电容充放电过程中存在的容-压滞回物理特性,本文提出一种准确提取超级电容等效内阻与容值参数的方法,基本原理如图2所示。由图2可知,在平衡充放电过程中,超级电容中电阻压降的极性随电流极性交替变化,即充电过程中压降为正而放电过程中压降为负,从而产生滞回特性。
3 实验验证
本文开展了一系列实验以验证基于充放电滞回特性的超级电容参数提取方法的可行性与有效性。
3.1 超级电容测试系统
本文选用奥威 2.7 V/3 000 F 超级电容单体进行充放电测试,被测超级电容基本数据如附录 B 表 B1 所示。超级电容测试实验平台如附录 B 图 B1 所示,通过软件编程可对超级电容进行多种充放电操作,包括恒压充放电、恒流充放电、恒功率充放电和基于仿真电流数据进行循环充放电等。测试平台有 CH1、CH2这 2个测试通道,电压范围为 0~5 V,电流范围为 0~500 A。此外,测试平台可以进行温升实验,温度测试通道共8个,通过温度传感器能采集单体的表面温度和两极温度。超级电容测试系统主要参数如附录B表B2所示。
3.2 不同温度条件下充放电测试
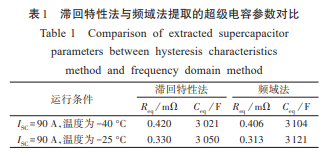
在不同温度条件下对奥威 3 000 F 超级电容进行 90 A 平衡充放电测试。利用滞回特性法对实验数据进行了处理,测得的超级电容内阻与容-压特性如图3所示。
为对比验证滞回特性法的正确性,本文同时采用频域法[21]提取了超级电容阻抗谱,实验结果如附录 B 图 B2 所示。频域法测量超级电容阻抗谱的基本原理是对循环充放电的超级电容端电压 USC 与电流 ISC信号进行快速傅里叶变换(FFT)分析,然后 计算不同频率下电容的等效阻抗,即 Zeq ( f )= fFFT (USC )/fFFT (ISC ),其中函数 fFFT表示对数据进行 FFT 以得到不同频率下的幅值,进而得到一定频段内的超级电容阻抗谱。频域法测得的阻抗谱下限频率由循环充放电周期决定,上限频率则主要受电压信号高频测量误差限制。以图 B2所示的 90 A 充放电测试结果为例,181 s充放电周期对应的阻抗谱下限频率为5.5 mHz,上限频率为5 Hz。阻抗谱可有效反映超级电容参数情况,其中低频段横、纵坐标分别近似等于超级电容内阻与等效电容,阻抗谱随频率变化趋势则反映出超级电容充放电过程中因多孔结构引起电荷再分布的动态特性。
相关知识推荐:论文排版怎么弄
不同温度条件下分别利用滞回特性法与频域法提取得到的超级电容内阻与容值的结果如表 1 所示,通过对比可得如下结论。
1)利用滞回特性法提取的电容内阻与频域法结果基本一致,验证了滞回特性法的可行性与有效性。温度对超级电容内阻有一定影响,特别当温度下降到-40 ℃ 时电解液粘度增加导致内阻增大,实验结果与理论分析一致。
2)不同温度下超级电容容值存在一定差异,滞回特性法与频域法结果的偏差量一致(约30 F)。在中高温区,提取得到的内阻随温度先减小后增大,其原因可能与该超级电容在中高温区的工作特性有关。实际系统中超级电容参数在中高温区的温度特性受具体结构、规格、材料等因素影响而呈现一定分散性[19]。
在精度方面,实际系统中滞回特性法应优于频域法。一方面,频域法的下限频率受循环充放电周期限制,在该频率下提取的超级电容等效参数与直流条件下的理论值不可避免地存在一定误差;另一 方面,频域法需要对电压、电流数据进行 FFT 处理,其精度易受信号平稳性、时间窗口周期性及采样率等因素影响。
3.3 不同电流条件下充放电测试
本文在室温环境(25 ℃)开展了不同电流条件下的平衡充放电测试并利用滞回特性法提取了超级电容内阻,结果如表2所示,可以发现超级电容内阻随着充放电电流的增加而减小。随着电流增加,超级电容充放电过程中带电离子游移进入多孔结构与电子电荷形成双电层电容的过程加快,内阻减小。理论分析验证了实验结果的正确性。实际系统中,准确获取不同电流条件下超级电容内阻可为优化系统充放电策略提供依据。
3.4 动态充放电测试
为进一步验证滞回特性法的有效性,在25 ℃条件下对奥威 3 000 F 超级电容开展了动态充放电测试,实验结果如附录B图B3所示。由图B3(a)可知,动态充放电前电容初始电压为 USC0=2.35 V,根据历史数据得到的容-压曲线可以确定初始电容为 Ceq0=2 950 F。在此基础上采用附录 A 图 A2 所示方法可以估算出不同充放电电流条件下电容器等效内阻和容-压特性。图 B3(b)中蓝色曲线是 90 A 时滞回特性补偿后测得的容-压特性,红色曲线是 350 A 时滞回特性补偿后测得的容-压特性。进一步分析可知:电流为90 A时,内阻估算结果与图3所示恒流充放电时结果一致;电流为 350 A时,受充放电频率等因素影响,内阻下降。实际系统中,开展动态充放电测试可有效提高不同工况下超级电容等效参数提取的效率。
4 结论
本文在研究超级电容充放电特性的基础上重点分析了容-压特性滞回现象,并根据该原理提出一种超级电容参数提取新方法。超级电容充放电过程中容-压滞回特性产生的根本原因是充放电电流产生的电容器内阻压降极性相反,据此可准确获取电容器参数信息。不同温度、电流以及动态充放电实验结果验证了该方法的可行性与有效性。
与传统方法相比,基于滞回特性的超级电容参数提取方法充分利用充放电过程中所有测试数据,可有效排除超级电容非线性特性影响并提高检测精度,适用于超级电容储能系统的性能测试、优化控制、高效运维等不同场合。附录见本刊网络版(http:∥www.epae.cn)。——论文作者:黄 鹤1,2 ,肖 飞1 ,杨国润1 ,麦志勤1
参考文献:
[1]赵洋,梁海泉,张逸成 . 电化学超级电容器建模研究现状与展望[J]. 电工技术学报,2012,27(3):188-195. ZHAO Yang,LIANG Haiquan,ZHANG Yicheng. Review and expectation of modeling research on electro chemical superca⁃ pacitor[J]. Transactions of China Electrotechnical Society, 2012,27(3):188-195.
[2] ASHTIANI C,WRIGHT R,HUNT G. Ultracapacitors for automotive applications[J]. Journal of Power Sources,2006,154(2): 561-566.
[3] BRENNA M,FOIADELLI F,TIRONI E,et al. Ultracapacitors application for energy saving in subway transportation systems [C]∥Proceedings of the 2007 International Conference on Clean Electrical Power. Capri,Italy:IEEE,2007:69-73.
[4] RUFER A,HOTELLIER D,BARRADE P A. Supercapacitor based energy storage substation for voltage compensation in weak transportation networks[J]. IEEE Transactions on Power Delivery,2004,19(2):629-636.
[5] 许爱国,谢少军,姚远,等. 基于超级电容的城市轨道交通车辆再生制动能量吸收系统[J]. 电工技术学报,2010,25(3): 117-123. XU Aiguo,XIE Shaojun,YAO Yuan,et al. Regenerating energy storage system based on ultra-capacitor for urban railway vehi⁃ cles[J]. Transactions of China Electrotechnical Society,2010,25 (3):117-123.
[6] 蔡国伟,陈冲,孔令国,等. 风电/制氢/燃料电池/超级电容器混合系统控制策略[J]. 电工技术学报,2017,32(17):84-94. CAI Guowei,CHEN Chong,KONG Lingguo,et al. Control of hybrid system of wind/hydrogen/fuel cell/supercapacitor [J]. Transactions of China Electrotechnical Society,2017,32 (17):84-94.
[7] 毕恺韬,安群涛,段建东,等. 基于级联多电平直流变换器的超级电容储能系统能量自均衡控制策略[J]. 电工技术学报,2018, 33(8):1919-1928. BI Kaitao,AN Quntao,DUAN Jiandong,et al. Self balancing control strategy for super capacitor energy storage system based on cascaded multilevel DC-DC converter[J]. Transac⁃ tions of China Electrotechnical Society,2018,33(8):1919-1928.
[8] 李轩,李永丽,常晓勇 . 基于精确线性化理论的超级电容储能系统的非线性控制算法[J]. 电工技术学报,2016,31(21):12-20. LI Xuan,LI Yongli,CHANG Xiaoyong. Nonlinear control algo⁃ rithm for super capacitor energy storage system based on exact linearization theory[J]. Transactions of China Electrotechni⁃ cal Society,2016,31(21):12-20.
* 稍后学术顾问联系您