0
发表咨询在线!

摘要: 设计了一种输电线路除冰机器人的机械结构, 分析了该机构的作业空间问题. 在计算过程中, 引入Monte Carlo方法得到了机器人操作臂的工作空间. 采用该方法可避免对机器人运动方程的求逆解计算, 极大地简化了计算过程. 分析并指出传统的机器人工作空间边界提取方法精度有限, 且存在理论上的缺陷; 提出了一种新的基于局部点象限分布的边界点提取方法, 文中给出的算例表明, 该方法不仅精度高, 并且非常适合于处理机器人工作空间边界问题.
关键词: 输电线; 除冰机器人; 工作空间; 蒙特卡罗方法
1 引言(Introduction)
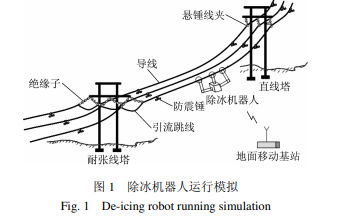
和传统的除冰方法相比, 采用机器人除冰具有功耗小、成本低、效率高、人员无伤亡、无需停电和可连续作业等优点. 作为一种可替代人工作业的输电线路在线除冰技术, 其发展前景非常广泛[1∼3] . 图1所示为除冰机器人现场运行模拟图, 为了顺利沿输电线行走和完成线路除冰, 机器人需要跨越输电线路上出现的各种复杂障碍物.
机器人的工作空间定义为末端执行器在结构限制条件下所能达到的所有位置的集合, 它是衡量除冰机器人越障能力的一个重要指标. 为了便于分析, 首先需要确定机器人的工作空间范围. 目前较为常用的方法是解析法和数值分析法. 解析法是基于Jacobian矩阵计算运动学逆解以确定机器人工作空间的方法. 由于计算的复杂性, 该方法只能处理某些特定结构的机器人工作空间问题[4,5] . 相比之下, 采用数值分析法更为灵活、简便, 其中最具代表性的是文献[6,7]提出的基于随机概率的蒙特卡罗计算方法. 由于该方法无需对机器人运动方程进行求逆计算, 因此非常适合于分析机器人工作空间问题. 但是, 采用蒙特卡罗方法只能得到机器人工作空间的近似图形描述. 为了便于计算和分析工作空间大小, 文献[8]采用栅格法提取了机器人工作空间边界点, 并借助最小二乘拟合的方法求得了工作空间边界曲线的解析表达式. 但是, 文献[8]提出的边界点提取方法精度有限, 采用该方法提取的边界点只是实际边界点的一种近似表示. 文献[9]采用分段求极值的方法虽然能够准确的提取出边界点, 但由于算法本身的限制, 无法确定所有边界点的位置分布. 另外, 通过下文的分析可知, 即使成功提取到了所有的工作空间边界点, 采用上述两种方法处理机器人工作空间问题仍存在缺点和不足.本文将采用蒙特卡罗方法对设计的一种三臂式除冰机器人作业空间问题进行分析, 同时对机器人工作空间边界点的提取问题进行详细的讨论.
2 除冰机器人本体机构设计(Structure design of de-icing robot)
由于除冰作业的环境非常恶劣, 对机器人本体机构可靠性和运行的稳定性要求很高. 本文在综合考虑了国内外现有较为成熟的巡线机器人方案的基础上[1∼3] , 设计了一种三臂式除冰机器人结构, 如图2所示, 机器人本体部分由3个灵巧机械臂和中间箱体组成: 前、后臂结构相同, 分别由大、小臂和末端夹持器组成, 大臂与箱体连接处为肩关节, 根据越障需要可实现左右和上下灵活转动; 小臂为升缩手臂, 其长度可调, 大臂和小臂连接处为肘关节, 根据需要可上下转动; 中间手臂为升缩臂. 各手臂末端为复合夹持机构, 同时具备驱动、夹持和除冰等功能, 其内部结构如图3所示. 夹持机构设计成可左右开合的结构, 输电线从夹持器中间穿过, 其前后水平横梁装有挂线滚轮, 以便于机器人挂线行走, 同时可降低夹持器对导线的磨损. 水平横梁随夹持器开合, 在闭合时利用楔子牢固连接两端,可起到防摔落作用. 夹持器内部设计有4个竖直的滚筒机构. 后端的一对为驱动滚筒, 其表面选用具有一定弹性、摩擦系数大的耐磨材料制成, 通过紧压电线, 可实现制动、行走等功能. 前端的一对为除冰滚筒, 其横截面做成突齿结构, 可实现碾压式除冰的功能, 为防止除冰时损伤电线, 除冰滚筒外部间距略大于电线外径. 两组滚筒中间装有扫冰刷, 用来扫除电线上的残余碎冰. 另外, 在夹持器前端装有除冰锤, 通过一个电子凸轮机构拉动弹簧带动除冰锤反复快速敲击覆冰, 在一定程度上把覆冰击碎或击松, 提高整个机构的除冰效率. 夹持器与手臂的连接处为腕关节, 用于机器人夹持机构的姿态调整. 中间箱体用于安放电源箱和控制箱.
机器人采用悬挂抓线的运动方式. 为了保证运行的稳定性, 在越障时应确保始终有两个手臂悬挂在线路上. 为此, 本文设计了三手臂依次脱线越障的方式, 其中, 中间手臂主要起稳定重心的作用, 前、后手臂为越障臂, 其末端夹持器所能到达的所有位置的集合即代表了机器人的工作空间. 为了便于分析, 以肩关节为原点, 机器人本体和输电线所在竖直平面为X-Z轴, 建立如图4所示空间参考坐标系.
对于图4所示空间二连杆机构, 根据D-H参数法[10]求得在参考坐标系下用关节变量θ表示的工作点P的位置向量:由于实际结构的限制, 关节变量θ1, θ2是在一定范围内变化的; 另外, 为避免除冰机器人作业时损坏输电线路上金具器件, 在设计过程中通常对关节关量活动范围加以限制以确保一定的安全作业空间.
3 基于 Monte Carlo 方法的 工作空间求解 (Solving the workspace based on Monte Carlo method) Monte Carlo
方法是一种借助于随机抽样来解决数学问题的数值方法. 对于图4的模型, 在变量允许变化范围内, 通过随机抽取的一组变量值 {(θ1)i , (θ2)i ,(a2)i}, 可以确定一个工作空间位置坐标值Pi , 当抽取的样本容量N足够大时, 由点集合{Pi}(i = 1, 2, · · · , N)即可近似的描绘出机器人的工作空间, 并且所取的随机点数目越多, 得到的工作空间就越精确, 形状也越清晰. 具体求解步骤为:
Step 1 求机器人的运动学正解, 确定机器人末端执行器在参考坐标系中的位置方程, 如本文式(1) 所示;
Step 2 在关节变量的变化范围内, 依次生成N 个均匀分布的随机值, 从而可得到N组变量值的组合;
Step 3 将随机生成的N组变量值代入所求得的位置方程, 得到N个末端执行器的坐标值, 将其对应的坐标值分别存入指定的矩阵中;
相关知识推荐:机器人领域普通期刊推荐
Step 4 将所求得的位置点显示出来, 即形成了机器人手臂工作空间点集的“云图”. 图5和图6分别为本文采用Monte Carlo方法求得的除冰机器人前臂在X-Z平面和空间平面内的工作空间图形(N = 6000).
4 工作空间边界的提取(Extracting boundary of workspace)
基于Monte Carlo方法只能得到机器人工作空间的近似图形描述. 为了便于计算和分析工作空间的大小, 准确地提取出工作空间的边界点是非常关键的步骤, 目前较为常用的方法是栅格法和极值法[8,9] .
4.1 栅格法(Grid method)
如图7所示, 栅格法的主要思想是: 将工作空间划分为N个离散的正方形网格, 将每个单元赋0或1; 如果单元包含有工作点, 单元值赋1, 否则赋0. 通过分析边界单元的特点, 可得如下判别条件: 如果与目标单元相邻的8个单元至少有1个为0, 同时目标单元为1时, 该单元为边界单元, 此时可以用单元内点集的平均坐标近似的表示边界单元点坐标.
显然, 采用栅格法提取到的边界点只是实际边界点的一种近似表示. 图8所示为提取的边界点在实际工作空间中可能的3种位置分布(阴影区域为实际工作空间).
4.2 极值法(Extremum method)
如图9所示, 将工作空间按列划分, 线段AB, CD 之间区域为一列, 宽度为∆L. 找出该区域内Z坐标方向上的极大值点a和极小值点d, 这两点即为该区域的上、下两个外边界点. 如果该区域存在内边界, 通过搜索极值的方法则无法找到内边界点, 这时可采用的方法是: 将该区域内点Z坐标方向按从大到小顺序排列, 然后逐点判断两个相邻点沿Z方向的差值是否大于预先设定的一个判别值. 如果存在大于该判别值的两点, 则说明该区域内存在内边界, 并且该相邻两点即为内边界点(如图9所示b, c两点).
显然, 采用分段求极值的方法只能提取部分边界点. 如果提高搜索精度(缩小∆L), 提取到的边界点集就越接近实际边界. 但是, 即使成功地提取出了所有边界点, 仍然难以准确地拟合出机器人工作空间, 这主要是由于随机产生的边界点不可能完全拟合实际边界造成的. 对于同一段离散边界点, 其可拟合成的曲线形式往往是不确定的. 分析如下:
图10所示为截取的一段工作空间, 点a, b, c, d和 e是该区域内连续相邻的边界点. 则描绘机器人工作空间的真实边界曲线形状有可能是如图11所示两种情形之一: 1) 真实边界未包含b, d两点; 2) 真实边界包含b, d两点.
一般来说, 机器人末端执行器的工作轨迹在小范围内应是光滑的, 比较图11两种情况, 左图更真实的反应了机器人实际的工作空间形态, 随机产生的边界点b, d并未拟合实际边界. 因此, 在提取和分析机器人工作空间边界问题时, 对于类似于b, d类型的边界点最好能当成内部点来处理, 显然, 采用传统的边界点提取方法无法处理这种情况.
表2为采用栅格法和极值法的计算结果. 当随机点数量较少时, 采用栅格法和极值法的提取精度要明显低于本文算法的提取精度; 随着随机点数目的增加, 两种方法的提取精度有所改善, 但总体来说, 二者精度要低于本文的提取方法. 另外, 根据图8所示栅格法提取到的边界点位置分布特点, 对于本算例圆形边界的工作空间, 基于栅格法计算得到的空间面积应略小于理论值, 表2中计算结果与理论分析的结果是一致地.
图13为采用本文方法提取到的图5所示工作空间的边界, 计算样本数N取10万个点, 可见, 采用本文方法提取到的边界具有较好的拟合度和光顺性.
6 结论(Conclusions)
1) 设计了一种三臂式除冰机器人结构, 研究了该机构的作业空间问题. 在计算过程中, 引入Monte Carlo方法计算机器人的工作空间, 避免了直接对机器人运动学方程的求逆解过程, 简化了计算.
2) 针对原有边界点提取方法的不足, 提出了一种基于邻域点象限分布的边界点提取方法, 和原有的方法相比, 本文的方法不仅精度高, 并且可以较好的处理机器人工作空间点云中的“虚假边界点”.
3) 以目标点为原点建立空间坐标系, 将搜索域改为球形域. 基于邻域点象限分布的边界点提取方法可推广到3维空间边界点的判定. ——论文作者:印 峰, 王耀南, 余洪山
参考文献(References):
[1] 李恩, 梁自泽, 谭民. 约束条件下的巡线机器人逆运动学求解[J]. 控制理论与应用, 2006, 23(1): 44 – 48. (LI En, LIANG Zize, TAN Min. Analysis of solution to the inverse kinematics of inspection robot for power transmission lines with constraints[J]. Control Theory & Applications, 2006, 23(1): 44 – 48.)
[2] POULIOT N, MONTAMBAULT S. Geometric design of the Linescout, a teleoperated robot for power line inspection and maintenance[C] //2008 IEEE International Conference on Robotics & Automation. Pasadena: IEEE, 2008: 3970 – 3977.
[3] 周风余, 李贻斌, 吴爱国, 等. 高压巡线机器人的设计与实现[J]. 机械科学与技术, 2006, 25(5): 624 – 626. (ZHOU Fengyu, LI Yibin, WU Aiguo, et al. Design and implementtation of inspection robots for high voltage power transmission lines[J]. Mechanical Science and Technology, 2006, 25(5): 624 – 626.)
[4] WANG Y F, CHIRIKJIAN G S. A diffusion-based algorithm for workspace generation of highly articulated manipulators[C] //Proceedings of IEEE International Conference on Robotics & Automation. Washington: IEEE, 2002: 1525 – 1530.
[5] CHEN X, GUPTA K C. Geometric modeling and visualization of manipulator workplace[J]. ASME Computers in Engineering, 1991, 1(5): 469 – 474.
[6] RASTEGAR J, PEREL D. Generation of manipulator workspace boundary geometry using the Monte Carlo method and interactive computer graphics[J]. ASME Journal of Mechanical Design, 1990, 112(3): 452 – 454.
[7] RASTEGAR J, FARDANESH B. Manipulator workspace analysis using the Monte Carlo method[J]. Mechanism and Machine Theory, 1990, 25(2): 233 – 239.
[8] ALCIATORE D, NG C. Determining manipulator workspaceboundaries using the Monte Carlo method and least squares segmentation[C] //23rd ASME Mechanisms Conference. Minneapolis: ASME Press, 1994: 141 – 146.
[9] 曹毅, 李秀娟, 宁祎, 等. 3维机器人工作空间及几何误差分析[J]. 机械科学与技术, 2006, 25(12): 1459 – 1502. (CAO Yi, LI Xiujuan, NING Yi, et al. Computation and geometrical error analysis of a 3D robot’s workspace[J]. Mechanical Science and Technology, 2006, 25(12): 1459 – 1502.)
[10] 熊有伦. 机器人技术基础[M]. 武汉: 华中科技大学出版社, 2008.
* 稍后学术顾问联系您