0
留言稍后联系!

摘 要:针对高压输电线除冰机器人工作环境的特殊性以及工作任务的复杂性,建立了机器人的运动学与动力学模型。在此基础上,通过采用粒子群算法对 PID 控制器三个参数进行在线寻优,实现了除冰机器人的运动控制。最后针对除冰机器人在斜坡爬行的情况进行仿真实验,证明了所设计的模型与运动控制方法的可行性。
关键词:除冰机器人;粒子群算法;运动控制;建模
1 引言
近年来,在俄罗斯、加拿大、美国、日本、英国、芬兰、冰岛和我国等众多国家,由于输电线路上的覆冰和积雪,常引起线路跳闸、断线、倒杆、绝缘子闪络和通信中断等事故,带来了巨大的经济损失。不仅如此,2008 年初中国南方发生的冰雪灾害还带走了数名电力工人的生命。研究输电线路除冰机器人替代传统的人工除冰对于保护电网的安全运行和电力工人的生命安全都具有极其迫切的现实意义。
除冰机器人工作在架空柔性输电线上底座悬空,主要依靠悬挂在线路上的手臂运动来改变机器人本体的位置和姿态。因此传统的地面移动机器人建模和路径规划方法不再适用于除冰机器人。与除冰机器人类似的自由空间飞行机器人 FFSR 工作在空间微重力环境下,基座处于自由漂浮状态。Y.Umetani 和 K.Yoshida 对整个机器人系统引入动量守恒定律,提出反映 FFSR 微运动学的广义雅克比矩阵(GJM)[1];R.Mukherjee 和 Y. Nakamura [2],K.Yamada 和 K.Tsuchiya [3],Y.Yokohji 和 T.Toyoshi- ma[4]等人采用不同方法也都推导出了 GJM,并通过对 GJM 分析,将其分析结果应用到各类控制方法中实现了机器人的路径规划。此外,Z.Vafa 和 S.Dubowsky 提出虚拟机械手的概念用来描述 FFSR 的几何结构[5],提供路径规划方法。E.Papadopoulos 和 S.Dudowsky 提出了基于拉格朗日方程的动力学模型[6],从而实现路径规划。S.K.Saha[7]提出一个通用建模方法,并将结果用以实现路径规划。此外,高压输电线巡检机器人的研究也为除冰机器人的研究提供了理论依据[8]。
针对高压输电线除冰机器人工作环境的复杂性以及工作任务的特殊性,首先结合研究机器人动力学和运动学问题,实现了对机器人的数学建模,再运用基于粒子群优化控制参数的 PID 控制器,对除冰机器人进行运动控制。最后针对除冰机器人在斜坡上爬行的情况进行了实验仿真,结果验证了所设计模型和运动控制方法的可行性。
2 除冰机器人模型分析
2.1 除冰机器人结构
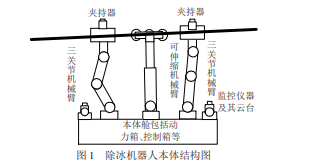
由于除冰机器人工作要求以及工作环境都很特殊,设计除冰机器人的结构如图 1 所示。首先为了保障机器人的可靠性与灵活性,设计为 3 臂结构,其中前后两臂为三关节机械臂,中间机械臂为可伸缩臂,其末端夹持器都安装有主驱动轮和从动轮,用来驱动和保持机器人平衡,并配备有除冰机构和抱死机构,以保证除冰、行进、夹持电缆、防滑等功能,这是同巡线机器人相比结构上最大的不同。为了保障除冰机器人安全工作,在本体舱上配置有监控仪器,对除冰机器人运行状态进行实时监控并返回状态信息。同时,在本体舱的动力箱为机器人提供稳定工作的动力,保障动力的稳定性与持久性,使用的动力为混合动力(小型汽油机+蓄电池),是保障除冰和行进同时进行的必要保障,也是巡线机器人动力所不能及的。本体舱内还有控制箱,控制箱主要由工控机和众多的外围设备等构成,对机器人运行状态进行实时控制,特别是除冰控制是巡线机器人空缺的功能。
2.2 除冰机器人模型的建立
在建立除冰机器人模型之前,先做如下约定:(1)除冰机器人左右臂关节均为转动关节;(2)假设机械手在运动过程中严格遵守动量守恒定律、力平衡和动量平衡定律;(3)系统全部由刚性构成。在满足以上约定的前提下,建立除冰机器人的几何模型如图 2 所示。
其中符号约定如下:mij:第 j 个机械臂的第 i 个连杆的质量,其中 i=1,2,3,j=b,(分别表示后臂和前 f 臂);m0:本体舱质量;mm:中间臂质量;pij:机械臂末端效应器在惯性坐标系中的位置向量;aij:机械臂连杆坐标系中,从关节 i 指向连杆 i 质心的位置向量;bij:机械臂连杆坐标系 i 中,从关节 i 质心指向关节 i+1 的位置向量;lij:机械臂连杆坐标系 i 中,从关节 i 指向关节 i+1 的位置向量;准ij:第 j 个机械臂的第 i 个连杆与水平方向所成的夹角;α:输电导线与水平方向所成的夹角。
4 检验与仿真
除冰机器人模型各参数如下:本体舱为长 0.8 m,宽 0.6 m,高为 0.6 m,重为 15 kg 的长方体,机器人左右两臂对称,第一连杆和第二连杆都长为 0.3 m、重 1 kg,第三连杆长为 0.2 m、重 0.5 kg,中间臂长最大值为 0.8 m,最小值为 0.5 m,重为 1.5 kg。输电导线与水平方向所成角度为 a=0.5°,轮子半径为 r=0.025 m,两轮的水平间距都为 0.25 m,中间伸缩臂长为 0.65 m。
通过运用 PSO 算法优化参数后的 PID 控制器对除冰机器人进行控制,其仿真实验结果如下。
从图 5 可知,用 PSO 算法优化参数后的 PID 控制器能够绝对逼近加速度曲线。从图 6 也可以看出,其速度曲线的逼近程度也很好。此外,通过图 7 可以直观地看到加速度误差在 5% 以内。实验结果说明,运用所建立的模型,再经过 PSO 算法优化参数后的 PID 控制器控制,能够实现对机器人的精确运动控制。此外,用 BP 神经网络参数优化 PID 控制器,得到的速度和加速度误差分别为 9.8%和 10.3%,远大于 PSO 算法优化模型。
5 总结
就高压输电线除冰机器人工作环境的复杂性以及工作任务的特殊性考虑,结合考虑了机器人运动学和动力学问题,对机器人的数学建模。并根据建立的模型,运用基于粒子群优化控制参数的 PID 控制器,对除冰机器人进行运动控制。最后针对除冰机器人在斜坡上爬行的情况,进行了实验仿真,结果验证了所设计模型和运动控制方法的可行性。——论文作者:张海霞,孙 炜,缪思怡
参考文献:
[1] Yoshida K,Umetani Y.Control of space free flying robot [C]//Proc IEEE Conf Decis Control,1990,90:97-102.
[2] Mukheijee R,Nakamura Y.Formulation and efficient computation of inverse dynamics of space robots[J].IEEE Transactions on Robotics and Automation,1992,8(3):400-406.
[3] Yamada K,Tsuchiya K.Efficient computation algorithm for manipu- lator control of a space robot[J].Soc Instrument Contr Eng Trans, 1990,26(7):765-772.
[4] Yoshida K.Experimental study on the dynamics and control of a space robot with experimental free -floating robot satellite(EEO- FORTS) simulators[J].Advanced Robotics,1995,9(6):583-602.
[5] Vafa Z,Dubowsky S.The kinematics and dynamics of space ma - nipulators:The virtual manipulator approach[J].The International Jour- nal of Robotics Research,1990,9(4):3-21.
[6] Papadopoulos E,Dubowsky S.On the nature of control algorithms for free-floating space manipulators[J].IEEE Trans Robotics Automat, 1991,7(5):750-758.
[7] Saha S K.A unified approach to space robot kinematics [J].IEEE Transactions on Robotics and Automation,1996,12(3):401-405.
[8] 张运楚,梁自泽,谭民.架空电力线路巡线机器人的研究综述[J].机器人,2004,26(5):467-473.
[9] 朱兴龙,王洪光,房立金,等.输电线巡检机器人行走动力特性与位姿分析[J].机械工程学报,2006,42(12):143-150.
[10] 郭琦,洪炳蓉,吴葳.双臂六自由度空间机器人广义雅可比矩阵的推导[J].电子学报,2005,2(2):322-326.
[11] 周风余,李贻斌.高压输电线路自动巡线机器人机构设计及在约束条件下的逆运动学分析[J].中国机械工程,2006,17(1):4-9.
[12] Silva G J,Datta A,Bhattacharyya S P.New results on the synthe- sis of PID controollers[J].IEEE Transactions on Automatic Con - trol,2002,47(2):241-252
* 稍后学术顾问联系您