0
发表咨询在线!

摘要: 众包配送平台通过集结社会闲散运力为应对激增的外卖实时配送需求提供了新的思路,其核心的订单分配与路径优化问题作为影响其配送成本与效率的关键问题受到关注。针对该问题中订单的实时性、时效性、配送员的自由性等特征,建立以平均每单配送距离以及平均每单完成时间最小为目标的实时订单分配与路径优化模型。分别设计了贪婪策略、最小差值策略用于求解该问题。最后通过大量的数值仿真研究验证了两个策略的有效性,发现最小差值策略所得的平均每单配送距离更短,而贪婪策略所得的平均每单完成时间更短。进一步研究了两种策略在不同配送员容量限制、配送员数量、订单密度等参数变化时的适用性,需要控制成本宜采用最小差值策略,追求配送效率宜采取贪婪策略,研究结果可为众包配送平台的订单分配与路径优化策略的选择提供决策支持。
关键字:实时配送;订单分配;路径优化;众包平台;外卖
1 引言
近年来,中国外卖市场规模激增,2019 年的外卖用户已超过 4 亿人,对末端配送提出了严峻的考验。在最后 3 公里的配送能力与服务质量成为制约外卖市场发展瓶颈之际,美团、京东众包等众包配送平台迅速崛起,通过集结社会闲散运力,为解决外卖实时配送难题提供了一条新的途径。
顾客在美团、饿了么等众包外卖平台上下单,商家通过平台接受订单,同时商家通过平台发布配送需求订单信息,包括取送货地点、货物种类数量和预计配送时间等,平台通过订单分配的方式或让配送员抢单的方式将配送订单分发给相应的配送员,每个配送员具有车容量限制,且其工作时间与开始工作的地方具有绝对的自由。每个配送员接受相应的配送订单后需要到商家取货后送达至顾客以完成配送订单。在该过程中,由于配送订单的发布具有实时性,每个订单都要求在尽可能短的时间内完成,即具有很强的时效性,且每个订单的取送货地点一一匹配。同时考虑到高峰期配送订单数量庞大、地理位置分散、配送员具有动态性且随机分布等特点,要寻求配送成本低、顾客满意度高的订单分配与路径规划方案具有极大的挑战性。本文针对基于众包平台的外卖实时配送问题的上述特征,研究以降低配送成本、提高配送时效为目的的实时订单分配与路径优化科学问题。
与基于众包平台的外卖实时配送问题相关的文献包括众包配送服务问题和带取送货的动态车辆路径问题(Dynamic Vehicle Routing Problem with Pickup and Delivery)的相关研究。
针对众包配送中的服务组合和路径优化问题,南飞雁[1]研究了众包配送中的服务组合问题,采取 k 聚类算法先组合订单后分配,有效降低配送人员即时抢单导致的订单人均分配不均、超时等问题。李占强[2]研究了众包配送中服务匹配与优选问题,建立匹配机制和灰色关联度服务评价的模型分别优化匹配机制和服务质量。针对动态取送货车辆路径问题,程月娇等[3]考虑静态和动态的接单模式,设计一种基于用户出行信息的订单匹配方法,并用蚁群算法求解。张力娅等[4]以顾客满意度和配送成本为目标函数,建立了考虑客户优先级的、带时间窗的、动态的、多车场取送货车辆路径模型,用改进的迭代局部搜索算法求解。张旭梅等 [5]以随机动态环境下运输过程中的装卸混合问题为研究对象,根据随机动态装卸混合问题的实际应用分别将车辆数由单车辆推广至多车辆、目标函数由单目标推广至多目标、“需求服从均匀分布”的假设条件放宽为“需求服从一般分布”进行讨论,针对各情形提出了相应的求解策略,对各求解策略进行了渐近性分析,并对其求解效果进行了仿真。张玉州等[6]以外卖配送服务总延误时间最短为目标,设计了一种基于滚动时域控制的外卖配送问题模型,用最近邻域算法求解,并以实际案例对比 FCFS 和 NN 算法。李桃迎等[7]以外卖配送成本增量总和为目标函数,并考虑了随机参数对计算复杂度的影响,用 R 语言测试模型和算法。宁涛等[8]以最小化成本和最大化客户满意度为目标,把动态车辆路径问题转换为静态车辆路径问题,采用两阶段建模,用改进的量子蚁群算法求解。魏瑛琦[9]针对动态车辆路径问题,采用两阶段建模方式,将动态车辆路径问题转化为静态车辆路径问题,采用时间片段原则处理动态事件,用改进的量子蚁群算法求解。吴腾宇等[10]研究了带有取送货的在线旅行商问题 (Traveling Salesman Problem, TSP),针对需求点在不同网络上的情形分别设计了 TAIB 算法和 IGNORE 算法求解。Azi et al[11]针对多交付路线的动态车辆路径问题,设计一个自适应的大型邻域搜索启发式算法求解,在动态情况下将考虑发生未来请求的多个可能场景,以决定是否有机会将新请求包含到当前解决方案中,当车辆离开仓库时配送路线将被关闭。 Mitrovic-Minic et al [12]研究未来请求不能随机建模或预测的动态 PDPTW,分配新的请求时,最好考虑一项决定对短期和长期的影响,描述了基于双视界的动态 PDPTW 启发式算法。 Vonolfen et al [13]考虑在问题的动态变量中,不是所有的信息都是预先可以得到的,而是在规划过程中被揭示出来的,提出一种基于进化计算和模拟模型的直接策略搜索方法,针对不同的问题特征设计专门化等待策略。Branke et al [14]考虑一个动态车辆路径问题,让车辆在旅行期间在适当的位置等待以最大限度地提高额外客户被整合到其他固定旅游路线中的可能性,得到一辆车和两辆车的最佳等待策略。综上所述,在现有文献中,对一一匹配严格的动态取送货车辆路径问题的研究中针对模型和算法的文献较少,本文研究内容与以上文献的最大区别在于配送员的位置是动态随机分布的,本文研究的是基于众包外卖平台具有实时取送货、配送员随机分布等特点的现实问题。
综上所述,通过分析众包外卖即时配送的特点,以平均每单配送距离最小和平均每单完成时间最小为目标,构建基于众包平台的外卖实时配送订单分配和路径优化模型,针对不同应用场景,分别设计贪婪策略、最小差值策略用于求解该模型,旨在降低物流配送成本,提高配送效率。考虑了配送员数量、车容量、订单密度等参数对策略稳定性的影响,通过数值仿真实验验证模型和算法的有效性,并对设计的算法的优劣进行评价。
2 问题描述与建模
给定一个道路交通网络图𝐺 = (𝑉, 𝐸),其中顶点集合𝑉 = *𝑣1, 𝑣2, … , 𝑣𝑛1 +,边集合𝐸 = *𝑒1, 𝑒2, … , 𝑒𝑛2+,所有需要服务的订单均在网络图𝐺中产生,𝑙(𝑣𝑖 , 𝑣𝑗)表示网络图中𝑣𝑖与𝑣𝑗之间的距离,所有订单是实时产生的,共有𝑛个订单,订单序列表示为𝜎 = *𝑂1,𝑂2, … ,𝑂𝑛+,将产生的订单表示为𝑂𝑖 = (𝑟𝑖 , 𝑢𝑖 , 𝑑𝑖),其中𝑟𝑖表示订单需求的释放时间,𝑢𝑖 ∈ 𝑉表示订单的取货点位置,𝑑𝑖 ∈ 𝑉表示订单的收货点位置,𝑖 ∈ 𝐼 = *1,2, … , 𝑛+,考虑多个配送员进行配送服务,车容量均为𝐶,即每个配送员同时最多能为𝐶个订单服务,在外卖配送过程中,商家通过平台不断接受订单,平台会继续给配送员分配订单,要研究的问题是如何实时分配订单给对应的配送员,如何为配送员进行路径规划,使得平均每单的配送距离最小和平均每单完成时间最小。
为了研究的方便提出如下 4 条假设:假设 1:在网络图中每个点既可以是取货点又可以是送货点,但同一个点不能是一个订单的取货点和送货点;假设 2:当每出现一个新订单时,配送车辆需要到取货点取货然后送至送货点以完成该订单,不考虑配送员在该服务点的等待时间;假设 3:允许车辆在其初始位置或任何取、送货位置等待,配送完成后不必返回原起始位置;假设 4:配送员均以速度𝑣行进。
由于动态实时取送货车辆问题(Dynamic real-time pickup delivery vehicle problem, DRVRP)是 NP—hard 问题,运用精确算法求解在时间性能和求解规模等方面均存在局限性,考虑到该模型中的订单释放时间是不能提前已知的,所以无法设计最优化算法,故设计插入式启发式算法求解。基于此,对该问题提出两种求解策略,贪婪策略和最小差值策略,以下将分别对两种策略进行描述和分析。对各策略的稳定性和适用范围进行分析,以及参数与目标函数的关系进行仿真。
3 求解策略
下面将给出贪婪策略和最小差值策略,分析两种策略在随机参数变化的情形下的稳定性,并通过对目标函数配送员完成平均每单距离和平均每单完成时间的分析比较,分析两种策略在不同的应用场景下的有效性和适用性。
3.1 贪婪策略
核心思想:将新产生的订单分配给距离取货点最近的且满足车容量限制的配送员。其具体步骤如下:
第一步:当没有订单产生时,配送员在原始位置等待,当产生一个新订单时,转第二步;
第二步:计算新订单的取货点距离各个配送员的距离,将新订单分配给距离取货点最近的且满足车容量限制的配送员;
第三步:为新分配订单了的配送员规划路径;
(3.1)当配送员的配送路径中有𝑛个待服务的订单,即有2𝑛个点,配送员每接受一个新订单也会新产生两个点,将取货点插入原来的路径中的2𝑛 + 1个空点的任意位置;(3.2)然后将送货点插入在取货点以后的任意位置,计算每次插入送货点以后总的配送路径的距离;(3.3)比较所有插入方式所得到总的配送路径的距离,选取最小的距离所对应的插入方式插入新订单的取送货点,即配送员的配送路径。
3.2 最小差值策略
核心思想:将新产生的订单分配给以最佳插入方式插入所得到的配送距离与不插入状态下的配送距离的差值最小的且满足容量限制的配送员。
最小差值策略与贪婪策略的核心步骤区别如下:
第二步:用插入法将新订单的取送货点插入每个配送员的初始配送路径中,计算所有插入方式所得到的配送距离;
第三步:为新分配订单了的配送员规划路径;
(3.1)将所有插入方式所得到的配送距离进行比较,选取配送距离最小的最佳插入方式,计算将新订单以最佳方式插入和不插入状态下各个配送员配送距离的差值;(3.2)将各个配送员配送距离的差值比较排序,把订单分配给配送距离的差值最小的配送员,同时得到该配送员的最佳配送路径。
3.3 最小差值策略与贪婪策略框架图
4 数值仿真研究
为验证模型与设计算法的真实有效性,在此用数值仿真软件编程,采用贪婪策略和最小差值策略,分别使用插入式算法对算例进行数值仿真。实验采用数值仿真软件在 PC 机上运行(i5-3230M 处理器,4G 内存,Windows10 64 位操作系统)。
本文以重庆市南岸区南坪为中心点,向周围辐射 1.5 公里选取某些商家住宅小区的地理坐标为仿真研究网络图,以配送员平均完成每个订单所行驶的距离和所花费的时间为目标函数,分别从订单分配和路径选择两个模块进行策略的设计和算法的求解,通过设定不同参数(如车容量、配送员数量、订单密度)对目标函数的影响,找出对目标函数最为敏感的影响因素,分析不同策略在不同参数影响下的适用性以及策略在同一参数数值变化下的稳定性。参数设置:车容量𝐶为 6,配送员数量 为 6,订单密度(即是订单数量与仿真时间的比值)为 1.11 时是车辆装载率较好的基础参照数据,仿真时间为 180 分钟,仿真次数为 100 次,网络规模用给定的网络图中任意两点间距离的平均值𝑙为̅ 1.56 千米。
由表 2 第 3、9、16 行可知,采用贪婪策略,完成订单的平均时间约为 8 分钟,考虑商品制作时间 10 分钟,配送员取送餐上楼等时间 5 分钟,现实中的订单配送时间大约 30 分钟,两者差值约为 7 分钟,完成订单的平均距离约为 7.2 公里,考虑现实中配送距离约为 3 公里,来回大约 6 公里,两者差值约为 1.2 公里;采用最小差值策略,完成订单的平均时间约为 13 分钟,考虑商品制作时间 10 分钟,配送员取送餐上楼等时间 5 分钟,现实中的订单配送时间大约 30 分钟,两者差值约为 2 分钟,完成订单的平均距离约为 5 公里,考虑现实中配送距离约为 3 公里,来回大约 6 公里,两者差值约为 1 公里。他们的差值均在合理范围内,所设计的两种策略均有效。
由表 2 第 3 至 8 行可知,当增大车容量时,对于平均完成订单的距离而言,采用贪婪策略和最小差值策略均是先增大后减小,对于平均完成订单的时间而言,采用贪婪策略和最小差值策略均是先增大后减小,其方差极小,车容量的变化对目标函数的影响并不明显,可以忽略不计。由表 2 第 9 至 14 行可知,当增大配送员数量时,对于平均完成订单的距离而言,采用贪婪策略和最小差值策略均减小,配送员数量的变化对最小差值策略的影响略大于贪婪策略,对于平均完成订单的时间而言,采用贪婪策略和最小差值策略均减小,配送员数量的变化对贪婪策略的影响略大于最小差值策略;其方差较小,且配送员数量的变化对目标函数的影响较小,增大配送员数量在一定范围内可以减少订单的等待时间,可以通过增加一定的配送员数量降低配送成本同时提高配送效率。由表 2 第 15 至 20 行可知,当增大订单密度时,对于平均完成订单的距离而言,采用贪婪策略和最小差值策略均增大,对于平均完成订单的时间而言,采用贪婪策略和最小差值策略均增大,其方差波动明显,因此订单密度的变化对目标函数的影响极其不稳定,但订单密度增大,商品制作时间较长,平均完成每单的距离和时间也会相应的延长。
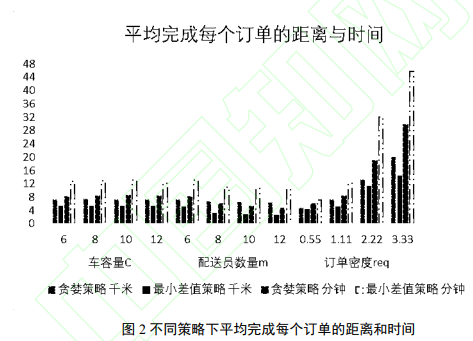
由图 2 可知,无论参数如何改变,对于平均完成每个订单的距离而言,贪婪策略总是优于最小差值策略,这是因为贪婪策略对实时订单的分配规则是将新产生的订单分配给距离取货点最近的且满足车容量限制的配送员;对于平均完成每个订单的时间,最小差值策略总是优于贪婪策略,这是因为最小差值策略对实时订单的分配规则是将新产生的订单分配给以最佳插入方式插入与不插入时两者距离差值最小的且满足容量限制的配送员。故而从商家角度出发,为了降低配送成本宜采用最小差值策略,从顾客角度出发,从配送时效看宜采用贪婪策略。
5 结论
针对众包平台的外卖即时配送订单分配与路径优化研究,以配送距离和配送时间为目标函数,建立了外卖即时配送车辆路径优化的 DRVRP 模型,并设计了贪婪策略和最小差值策略求解动态实时取送货车辆问题,通过数值仿真实验验证了算法的有效性。实验表明,对两种策略对比分析可以得出,在相同条件下,订单密度的变化对目标函数的影响比较明显,当车容量、配送员数量和订单密度增加时,对平均完成每个订单的距离而言,最小差值策略优于贪婪策略,这是因为最小差值策略的订单分配规则是将新产生的订单分配给以最佳插入方式插入与不插入时两者距离差值最小的且满足容量限制的配送员;对平均完成每个订单的时间而言,贪婪策略优于最小差值策略,这是因为贪婪策略的订单分配规则是将新产生的订单分配给距离取货点最近的且满足车容量限制的配送员。因此,从商家角度来看,为了降低配送成本宜采用最小差值策略,从顾客角度出发,从配送时效看宜采用贪婪策略,研究结果可为众包配送平台的订单分配与路径优化策略的选择提供决策支持。基于众包平台的外卖实时配送问题进一步还可以研究考虑配送员离开系统时间(即是配送员的工作时间)情形下的订单分配与路径优化问题。——论文作者:余海燕1,2*,蒋仁莲 1
参考文献
[1] 南飞雁. 众包配送中的服务组合研究[D]. 浙江理工大学, 2018.
[2] 李占强. 众包配送中服务匹配与优选问题研究[D]. 北京交通大学, 2018.
[3] 程月娇, 施炯, 黄彬. 众包物流环境下订单合并及配送路径优化方法研究[J]. 浙江万里学院学报, 2017, 30(4): 27-33.
[4] 张力娅, 张锦, 肖斌.考虑顾客优先级的多目标 O2O 外卖即时配送路径优化研究[J/OL]. 工业工程与管理:1-12. 31.1738.T.20200316.1854.002.html.
[5] 张旭梅, 陈久梅, 肖剑. 随机动态多车辆装卸混合问题及求解策略研究[J]. 系统工程学报, 2012, 27(1):61-68.
[6] 张玉州, 叶亮, 郑军帅. 基于滚动时域控制的动态外卖配送问题优化[J]. 计算机技术与发展, 2019, 29(10): 83-88+94.
[7] 李桃迎, 吕晓宁, 李峰, 等. 考虑动态需求的外卖配送路径优化模型及算法[J]. 控制与决策, 2019, 34(2): 406-413.
[8] 宁涛, 焦璇, 魏瑛琦, 等. 基于量子蚁群算法的随机需求的动态车辆路径问题[J]. 大连交通大学学报, 2018, 39(5): 107-110.
* 稍后学术顾问联系您