0
发表咨询在线!

摘要:地震波场可分解为三分量平动和三分量旋转运动. 旋转分量包含重要的波场梯度信息,是地震波场重建的关键要素,但过去由于缺乏稳定的高灵敏度旋转测量仪器,它在不同的地震学应用中常被忽略. 光纤旋转地震仪是率先打破测量仪器缺乏困境、最先实现商业化的旋转地震仪,也是目前最有发展前景的地震波旋转直接测量设备. 光纤旋转地震仪基于 Sagnac 效应,并依托成熟的光纤陀螺技术实现振动的旋转分量测量. 它具有纯光电传感不受平动影响的测量优势;并且能够在高灵敏度和宽频带旋转测量的基础下实现设备的小型化,有利于旋转测量的应用推广. 因此,光纤旋转地震仪和传统的地震仪将形成互补,实现旋转和平动六分量(6C)的观测,更好地提取地震波场特征,提高振动监测能力,有效改善震源过程反演、地下结构成像和地震破坏机理研究等应用. 本文主要介绍光纤旋转测量的基本原理、旋转地震学的应用及其潜在应用前景.
关键词:旋转和平动;旋转测量;光纤振动传感;光纤旋转地震仪;旋转地震学
0 引 言
地震学的发展建立在观测基础上. 无论是地震、塌陷、滑坡等天然事件,还是爆破或锤击等人工事件,都会产生包含平动和旋转的矢量振动波场,在介质中传播、散射和衰减. 地震观测的目的,就是在地下或地表有限观测空间中完整地记录介质中传播的振动波场,通过反演或成像,动态跟踪介质活动(如震源研究与地震监测)或精细探测介质结构(如浅层地震勘探和深部结构成像)(Sheriff and Geldart, 1995; Yilmaz, 2001; Aki and Richards, 2009). 因此,地震观测的首要任务是基于研究目标选择合适的地震仪器类型和数量,保障记录波场在空间(密集程度)、时间(采样率和持续时间)、振动矢量(单分量、三分量还是六分量)和频带等方面的采集需求.
目前地下介质动态监测和结构探测使用的地震仪,基本属于(弹簧)质量块惯性测量仪器(Havskov and Alguacil, 2016),单台只能测量平动. 其中地震长期监测和壳幔深部结构研究主要使用成本高的电容位移换能地震计(图 1a),具有灵敏度高、动态范围大、频带宽、稳定性和低频性能好的优点. 浅层地震勘探则主要使用动圈电磁换能高频检波器,虽然灵敏度、动态范围、频带、稳定性和低频性能都远远不如前者,但造价低、重量轻和体积小,容易大批量布设,适合于非常密集但运行时间不长的勘探应用. 近几年出现的廉价低功耗三分量节点式地震仪(王肃静等,2015;吴铁军, 2011),将检波器、电池和数字采集器等部件集成于一体,可以让空间密集采集能够连续观测一段时间.
现有介质监测或结构探测体系的一个明显不足,是缺乏高灵敏度振动旋转分量测量. 地震波的旋转分量,即经典弹性波动理论中的位移场旋度(Aki and Richards, 2009),与平动相比,可能更加微弱,但 却 是 完 整 地 震 波 场 的 不 可 或 缺 部 分 . Forbes (1844)制造出第一台有现代意义的地震仪时,就和同事提出测量角运动(旋转)的想法. 然而直到 100 多年后,才出现真正意义上可以测量地表旋转的地震仪(Nigbor, 1994; Sollberger et al., 2020). 虽 然 不 断 有 不 同 的 旋 转 测 量 仪 器 被 提 出 ( 如 Jaroszewicz et al., 2016), 包 括 六 分 量 地 震 仪(Brokešová et al., 2021; 图 1b),但目前商业化的旋转地震仪仍寥寥无几,旋转测量远未得到充分重视和广泛应用. 在缺乏观测的情况下,地震波的旋转分量在过去地震学研究中基本被忽略;对其在震源过程中的激发、在地震波能量中的占比、在介质中传播的特性和对建筑物的破坏等均缺乏深入认识.
现有地震观测体系的另外一个不足是缺乏可以长期持续密集监测的廉价设备. 很多应用领域都有高分辨率 4D 监测的强烈需求,如对断裂带、水库、滑坡和油气开采区等区域监测. 目前稀疏的地震台网难于满足 4D 精细监测的要求;而密集、持续的监测,即使是基于廉价节点式地震仪的密集观测,需要巨大的设备成本和维护成本. 在一些油气田应用中,常用间隔一段时间的重复 3D 地震勘探替代 4D 监测(如 Jack, 2017; Sambo et al., 2020). 这种观测方式可以达到较高的空间分辨率,但缺乏时间分辨率.
微机电系统(micro-electro-mechanical system, MEMS)的应用是未来廉价密集振动测量的一个发展方向. MEMS 的研发始于 1960 年代,它利用与集成电路相似的制造和精加工技术,将传感器集成至毫米—微米级的硅片上,具有体积小、重量轻、功耗低、可靠性高、易于集成和廉价等优点(Zhu et al., 2020). 现有技术可以将三分量平动(基于质量块惯性原理)和三分量旋转(基于科里奥利力效应)振动测量集成到一个芯片上(图 1c),常用于手机和运动手表等日常设备的振动和姿态检测;或通过集成内嵌,应用于建筑结构健康监测(Bońkowski et al., 2020)和传统地震计姿态的感知和矫正(D'Alessandro and D'Anna, 2014). 灵敏度和低频性能是 MEMS 在目前地震学应用的主要障碍. 通过灵敏度改进(Wang et al., 2020),目前已开始将 MEMS 应用于地震勘探领域,助力于百万 道 级 高 密 度 地 震 浅 层 勘 探 目 标 的 实 现 ( 如 https://www.sercel.com/products/Pages/DSU1- 508.aspx). 实验研究表明,MEMS 也可用于强震监测和地震预警,但目前尚不适用于常规的地震监测(D'Alessandro et al., 2019).
光纤传感是伴随着光纤加工和光纤通信技术的发展而成长起来的新型传感技术,已在很多应用领域取得了成功(方祖捷等, 2013; 张旭苹, 2013; Hartog, 2018). 光在光纤中传播,除了向前透射传播,还会产生向前(前向)和向后(背向)传播的散射光. 外部环境引起透射光或散射光走时、振幅或极性(偏振)等的变化,是实现光纤传感的基础. 光纤传感通常分为两类(张旭苹,2013):以引导激光进行传感测量(如激光干涉)的非本征传感和以光纤为传感部件的本征传感. 光纤振动传感是光纤传感的一个分支,应用于地震观测已有几十年的发展历史. 自 1980 年代以来,已提出多种不同的光纤振动测量方案并开展了相关实验(Davis, 1987; Gardner et al., 1987),目的就是希望在测量参数、性能、尺寸或价格等方面能够超越传统的地震计.
根据应用情景,我们可以将光纤振动传感分为如下四类(图 1d~1h):(1)传统弹簧—质量块惯性平动地震仪的的光纤换能测量改进(Huang et al., 2018; 图 1e);(2)基于 Sagnac 效应(或Sagnac 干涉,用法国物理学家 Georges Sagnac 名字命 名 , https://en.wikipedia.org/wiki/Sagnac_effect)的光纤旋转测量(Bernauer et al., 2018; 图 1f);(3)基于背向散射光的光纤分布式振动传感(distributed acoustic sensing,DAS,张旭苹,2013; Hartog, 2018; Zhan et al., 2020; 图 1g);(4)基于透射光相位(Marra et al., 2018; 图 1d)或偏振状态(Zhan et al., 2021;图 1h)变化的光纤振动传感. 前两类属于非本征光纤传感,后两类属于本征光纤传感.
第一类光纤传感主要用布拉格光栅等光纤设备替代传统的电容位移换能装置,提高地震仪的温压耐受能力或其它性能需求(Huang et al., 2018). 后面三类振动传感机理和传统地震仪完全不同:它们没有传统的惯性检测单元,是纯光电设备. 其中第二和第三类是目前最为成功的两类光纤振动传感技术. 光纤旋转地震仪被认为是目前最有发展前景的旋转测量设备(Jaroszewicz et al., 2016). DAS 以普通光纤为传感部件,利用光纤不同区段的散射光变化进行振动传感;一根光纤可以相对廉价地实现万道以上米级间隔的密集采集,有望成为未来密集长时监测的主力军. 第四类是近几年新提出的方法,利用光纤振动导致的透射光传播相位(走时)微弱变化或极性旋转检测振动,有长距离光纤监测的潜势(可超上万千米, Zhan et al., 2021b),但目前缺乏对振动的空间分辨能力.
可以看到,光纤振动传感是目前最有希望突破现有观测体系两大不足的观测技术;它们的改进和应用推广,对于地震学的未来发展非常重要. 因此,我们将用两篇文章分别介绍后三类光纤振动传感技术. 本文主要针对光纤旋转传感技术的基本原理、旋转地震学的应用及其潜在前景进行阐述和讨论.
1.2 旋转分量的测量方法
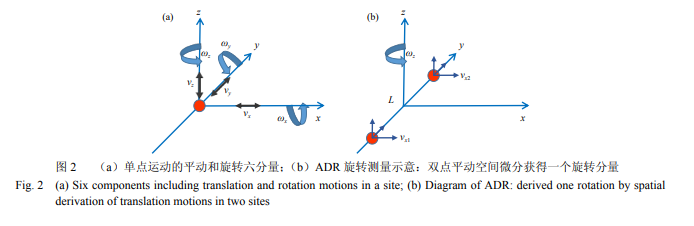
传统三分量地震仪的弹簧质量块被约束在三个正交坐标轴轴线内(即三个自由度),对质点运动的测量,相当于将它们投影到测量轴上,而原位旋转在测量轴没有投影,因此无法实现对旋转分量的测量(图 2a). 在过去的几十年中,基于机械扭矩、声学、电化学、磁流体和光学等原理,陆续提出了不 同 构 架 的 旋 转 测 量 仪 器 ( Jaroszewicz et al., 2016). 但由于实际研究对旋转地震仪的灵敏度、稳定性和动态范围等性能要求较高,大部分仪器仍然是实验室测试的原型机、野外样机或无法流动观测的大型设备(Jaroszewicz et al., 2016).
1.2.1 间接测量 ADR 方法
在没有旋转地震仪的情况下,可以用小孔径平动地震仪台阵间接测量介质旋转(array derived rotations, ADR. Spudich et al., 1995; Huang, 2003).
基于这种台阵间接测量的思想,Rotaphone 设备将多个水平和垂直分量检波器立体或平面排列组合安装在一个刚性三维框架或平面底盘上(图 1b 为其中一个最新的平面排列设计),利用三轴检波器和检波器对的平动差分,实现原位三分量平动和三分量旋转测量(Brokešová and Málek, 2010, 2020). Rotaphone 是目前少见的六分量(6C)一体化地震仪,但目前仍未商业化. 它将台阵微型化到较小的尺寸(直径 44.5 cm,高 11.2 cm),安装和携带性大幅提高,同时降低了场地和平动干扰的影响,但低频性能也有所损失;最近测试结果表明(Brokešová et al., 2021),Rotaphone 旋转测量分辨率可达 0.042 nrad/s,频率范围 1~20 Hz,动态范围达 120 dB,可以较好地满足地震高频旋转监测需求.
1.2.2 直接测量陀螺技术
陀螺是目前应用最为广泛的旋转直接测量技术,它的主要用途是惯性自主导航,因其自包含性强,不受外界干扰,是军事、航天和无卫星导航信号环境下的重要导航技术. 陀螺技术种类繁多,目前光纤陀螺技术较为成熟(图 3,薛连莉等,2020),在 旋 转 地 震 仪 中 使 用 最 为 广 泛 . Jaroszewicz 等(2016)对常见的各种旋转测量设备进行了比较,认为光学(特别是光纤)陀螺仪最适合于地震学观测应用,更有地学应用前景. 成熟的高精度和高稳定性光纤陀螺技术,促进了小型化旋转地震仪的商业化进程,将有助于旋转测量在全球的应用和推广,为地震学的发展带来深远的影响(Schmelzbach et al., 2018; Sollberger et al., 2020).
2 光纤旋转地震仪
光学陀螺基于光速不变原理,利用 Sagnac 效应测量旋转运动. 由于光子无质量,Sagnac 效应不受平动影响,可以测量净旋转分量. Sagnac 干涉测量示意图和原理如图 1f 和图 4 所示,将一束光分成传播路径相同、方向相反的两束光,最后返回到发射点形成干涉图像. 当光束所在平台没有转动时,两束光的到达时间相同、无相位差(图 4a);如果平台发生转动,与旋转同向的一束光走的路程要大于另外一束光(ΔL),两束光出现走时差(ΔT),它们的干涉条纹出现相位差(图 4b).
光纤旋转地震仪主要性能指标继承于光纤陀螺仪,但性能要求高于普通导航. 主要的参数如自噪声(和灵敏度有关)、动态范围和响应频率范围等除了度量单位外,类似于平动地震仪. 较特殊的参数是仪器的零偏、零漂和标度因子. 其中仪器标度因子是指不同频率输入和输出角速率的比值,类似于传统地震仪的仪器响应曲线. 零偏是输入角速度为零(即陀螺静止)时陀螺仪的输出量,理想情况下应该为地球自转角速度的分量. 零漂即为零偏稳定性,表示当输入角速率为零时,陀螺仪输出量围绕其零偏均值的离散程度. 温度和光纤偏振态是影响标度因子、零偏和零漂的主要因素. 通常需要温度控制或者温度补偿来改善测量精度,同时采用偏振滤波或保偏光纤消除偏振对零漂的影响.
Bernauer 等(2018)提出可实用的旋转地震仪至少应该满足动态范围、自噪声、稳定性和标度因子等方面的 8 个要求. 表 1 对比了几种光纤旋转地震仪的参数,可以看到 G-Ring 在自噪声、动态范围等方面优势明显,但设备面积太大难于广泛应用. 这些设备中,BlueSeis-3A 性能并非最佳,但却是全球首个(或目前仅有的)商业化可流动观测宽频三分量旋转地震仪(图 1f). Bernauer 等(2018)对该设备的多个指标进行实验室测试,认为可满足地震学应用要求,但存在过重、功耗过大等不足. Izgi 等(2021)进一步在室内用 6 台 BlueSeis-3A 做了一致性测试,认为它们的相关噪声、自噪声和震源方向等方面能够获得可靠和一致的结果,满足野外应用需求. 目前光纤旋转地震仪应用推广的主要障碍还是在于它相对昂贵的价格(数倍于传统宽频地震仪),还有待更多成熟商业化旋转地震仪的推出和竞争.
3 旋转地震学应用
旋转分量通常和平动分量组合应用. 包含旋转和平动的 6C 地震波矢量信息,能够有效地改善传统地震监测的性能,拓展平动观测的应用领域,从而在震源定位、震源机制和破裂过程等震源参数反演、地下结构成像、建筑抗震和健康监测等工程应用中发挥重要的作用.
3.1 地震监测性能改善
旋转测量可以在多个方面改善现有的地震监测性能. 首先是旋转可用于平动地震仪器的倾斜、去噪和方位校正. 传统地震仪对倾斜非常敏感. 在冻土、海底或火山等区域,地表隆起或下陷经常发生,导致仪器倾斜影响记录,甚至无法正常工作. 除了静态的倾斜变形,还有动态的倾斜影响. 风能够引起极低频(10~100 mHz)的倾斜变化(Venkateswara et al., 2017). 地震波的旋转分量,特别是在低频范围,会产生类似的动态倾斜,改变平动地震仪水平分量的重心投影,使它们的波形发生微弱的变化. 对火山地区的研究发现(van Driel et al., 2015),虽然动态倾斜效应导致的大多数地震台站记录的波形变化并不明显,但却显著影响了活火山近场超长周期(10 s 以上)事件的震源张量反演. 而通过理论模拟测试发现,将旋转分量数据加入反演,可以大幅度改善震源张量反演结果的准确性.
Lindner 等(2017)发现海底地震仪(OBS)受洋流或海底形变影响,5~13 s 水平分量被旋转振动严重干扰. 他们利用 OBS 内置光纤陀螺仪测量出旋转分量,去除交叉耦合,发现 10 s 水平分量的噪声频谱幅度降低可以超过 11 dB. Bernauer 等(2020a)观测到从实验室到野外环境下仪器倾斜对加速度测量的严重影响,并提出了两种利用旋转地震仪记录校正平动信号的方法. 他们认为火山、海底、近断层和城市地震工程应用中非常有必要使用 6C 振动监测.
旋转测量也可以解决井下地震仪和 OBS 绝对水平方位角的问题. D'Alessandro 等(2014)利用廉价的 MEMS 陀螺仪,在井下地震仪安装下降过程中同时进行旋转测量,在大部分情况下,可以将安装方位角误差控制在 2°以内.
旋转与平动的结合,将具有更强的波场矢量特征拾取能力,显著提升现有地震台站的监测性能. 单台 6C 记录能够实现类似小孔径台阵的功能,获得地震波瞬态的传播速度、方向和极性等波场特征,对于解决震源定位、事件分离等很多地震监测性能相关的问题非常有益.
例如,当有不同事件的波形在相近的时间经过地震台站时,单台 3C 观测基本无法区分这些信号,将会把这些事件当成一个事件对待,造成误判(图 5a, 5d). 利用提取的方位角和速度信息,6C 观测能够很好地分辨出从不同方位入射而且时间重叠的多个事件(如图 5b, Sollberger et al., 2017). 在地震台站分布稀疏的地区,常使用单台方法定位地震. 但 3C 平动数据测量背方位角存在 180°混淆的问题,只能推测其中一个方位再进行定位. 旋转信息不仅可以更好地约束区分方位相位,甚至还可以提高方位测量精度. 如 Taylor 等(2021)使用台阵 ADR 方法通过旋转信息估算诱发地震的背方位角,发现可以比台阵 S 波波束方法减少约 40% 的拟合误差.
6C 观 测 还 可 以 更 可 靠 地 识 别 波 形 类 型(Sollberger et al., 2017; Yuan et al., 2020). 如 P 波和 S 波的质点运动在 3C 观测系统中都是线性的,无法区别;而在 6C 观测中,利用 S 波有旋转分量这个特征,就可以实现波场震相分离或滤波(Sollberger et al., 2020). 如果将波场分离功能应用到地震波形后续震相(如深度震相,深部界面的反射、转换震相等),将可以更多地提取地震波走时信息,改善地震定位或层析成像地下介质的射线覆盖.
Li 等(2017)提出了利用旋转信息进行地震事件自动定位的逆时反投影方法,通过旋转运动附带的速度空间梯度信息和基于能量流的聚焦准则,解决了局部化问题,提高了地震定位和发震时刻反演的精度. Donner 等(2016)则提出更直接的方法,利用单台 6C 地震记录频散曲线提取速度结构,再通过射线参数确定地震的位置和深度. 这些研究为有效利用 6C 观测开展震源研究提供了基本的思路和实践依据.
3.2 震源参数反演和破裂过程研究
旋转测量对于地震震源的研究非常重要. 地震波旋转分量的产生和震源破裂过程有关. 仅考虑断层面的对称位错,Bouchon 和 Aki(1982)针对地下走滑和倾滑断层开展模拟,结果显示地震激发的旋转分量远弱于平动分量(例如,长 30 km 的走滑断裂位错 1 m 产生的最大旋转速度才 1.5×10−3 rad/s). Takeo(2006)利用类似的模拟试图解释 1997 年日本 Izu 半岛的震群(最大震级 5.7)观测记录,发现模拟结果中的旋转分量数倍低于实际观测值,而地震矩却大于观测值二个数量. 由此可见,实际地震中的旋转分量被严重低估,不能用简单的地震破裂模型来模拟.
旋转能量之所以被低估,可能与断层滑移速度的空间变化或断层的旋转应变有关. 目前已提出多种较为复杂的地震破裂模型,如断层几何形态的弯曲、受断层障碍体影响破裂滑移的转向或模式转换等(Aksenov, 2006; Majewski, 2006),试图定量解释地震时旋转分量的产生机理. 要有效地反演震源破裂过程或断层内部的不均匀性,迫切需要开展震源周边的旋转与平动 6C 测量.
近年来一些在震源区的 6C 观测也表明,旋转观 测 对 震 源 研 究 的 必 要 性 . Górski 和 Teisseyre (2006)发现冰川上的地震事件,特别在 0~5 Hz 的低频范围具有非常丰富的旋转分量,携带着冰川对复杂应力反应的新信息. Wassermann 等(2020)在夏威夷火山开展的单台 6C 观测,在三个方向均清楚记录到静态旋转,揭示出火山塌陷地震发生时介质复杂的运动轨迹. 从理论合成数据至野外实际数据,不同的研究都表明,如果能够包含旋转运动数据,震源反演精度,特别是矩张量和矩心深度的分辨率,将能够得到显著的提高(Bernauer et al., 2014; Donner et al., 2016; Reinwald et al., 2016);甚至可以从单台 6C 观测获得震源矩张量信息(Donner et al., 2018). Donner 等(2020)用朝鲜半岛的一个核爆和一个天然地震的合成数据,对比了 1D 和 3D 速度结构,3C 和 6C 数据 4 种组合下矩张量的反演,发现总体而言,6C 数据的参与可以改善反演结果;特别是当提高反演频率范围时, 3D 和 6C 组合会有更显著的反演分辨率改善(图 6).这给以高频能量为主的 M<3.5 地震的矩张量可靠反演带来希望.
Yuan 等(2021)利用 2D 和 3D 合成数据说明在已知断层大概位置的情况下,仅用单台 6C 观测记录就能够恢复地震破裂路径和破裂速度;而当有 2 个以上台站的 6C 观测时,可以在无断层先验知识的情况下恢复破裂的时空图像. Yuan 等(2021)的研究并没有使用传统的 P 波信息,而是通过 6C 波场分离,示例使用 S 波记录反演地震破裂过程. 他们还利用高速路上的汽车振动信号,验证了单台 6C 观测反演的可行性(图 7).
3.3 旋转分量的传播特征和地下介质结构成像
6C 观测类似于台阵功能的波场分解和重构能力,有益于地下结构方面的研究. 受各向异性、P/S 波相互转换、波阻抗界面、散射体和场地的影响,地表接收到的地震波场往往比较复杂、相互干扰;有效的波场分离或压制,能够更好地分析波场传播特征,或提高地震成像分辨率和可信度.——论文作者:王伟君1*,陈 凌2,3,王一博4,彭 菲1
* 稍后学术顾问联系您